Compound interest accelerates the growth of savings and investments over time. The definition of compound interest is – the interest earned on an investment or savings account is reinvested into that same account, earning even more interest.
The earlier an individual starts investing and saving, the more years there are to take advantage of compound interest.
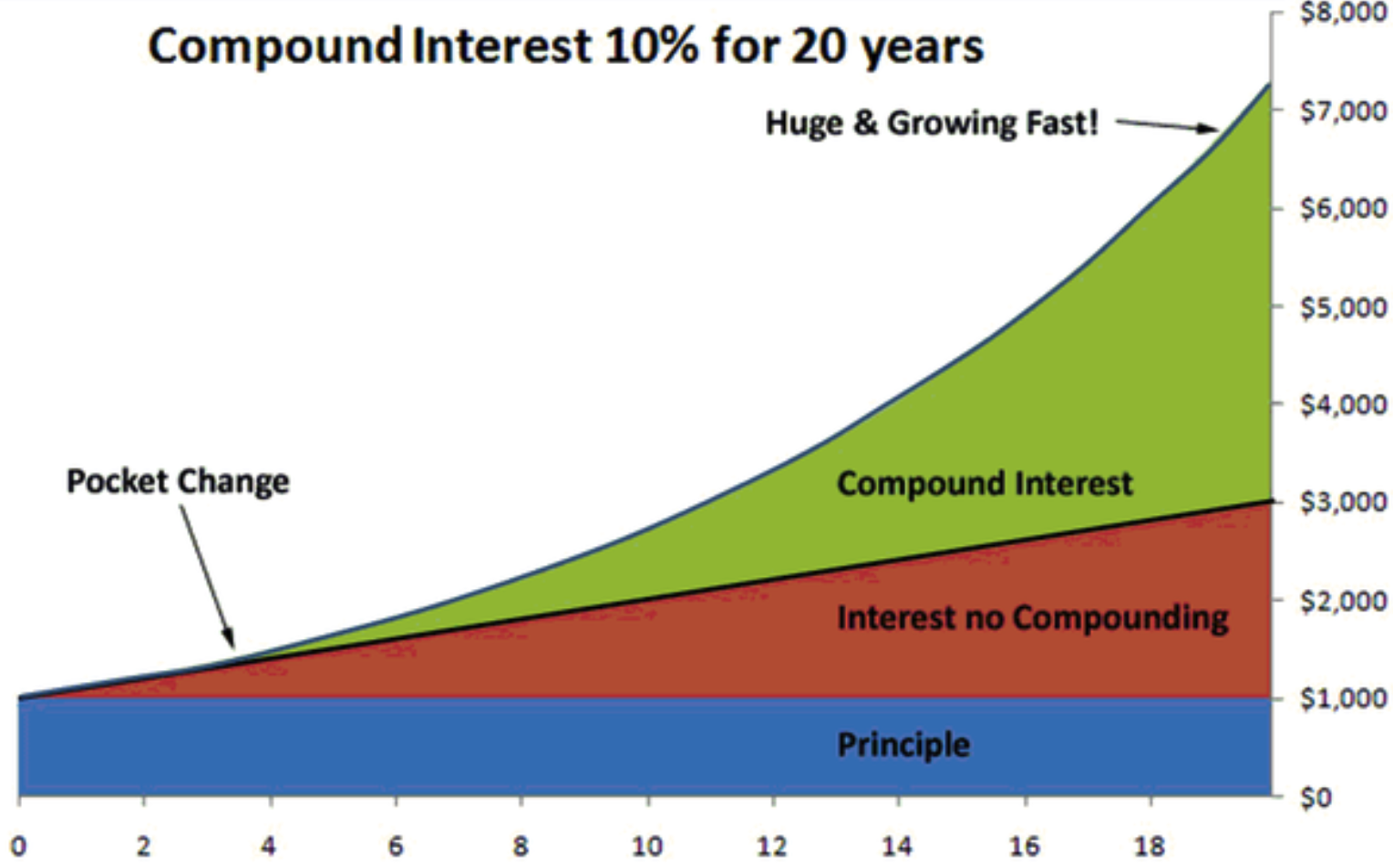
For example: if $1000 dollars is deposited in the bank. If the bank pays 10% interest annually, but it does not get reinvested, then after 20 years, that $1000 deposit is worth $3000 (see the red area on the graph below). This is called “simple interest .” If the interest is compounded, meaning it is added to the principal, and then the total amount continues to earn 10% interest, then after 20 years, you would have about $7200. The more frequently the interest is compounded or added to the total, the higher the final number is.
Here is an example of compounding frequency. In year one, 10% growth of $1000 savings is $100. If that $100 is moved in with the principle at the end of one year, it doesn’t start earning more money for a year. However, if the bank compounds every three months or quarterly, then after three months, $25 is deposited, and that money goes right to work earning money. Three months later, the amount earned will be slightly above $25, and that continues. You are making 10% of an increasing number. When you are considering an investment or savings account, it’s always good to ask the frequency that interest is compounded. The frequency may be anything from daily to annually. The higher the frequency, the more your money will earn.
If there is one example to demonstrate the importance of getting started early in investing, it illustrates the magic of compounding, as in the graph above. When your money earns more money, and then the money your money earns makes money, this, in a nutshell, is compounding. In the above compounding graph, the upward curve steepens over time, showing that the money grows faster with time (see the green section of the above graph). This is called exponential growth, which means increasing at an increasing rate. This is another reason compounding is a great thing for an investor
Compounding can work in reverse as well, which is a regrettable situation. If a person has a $1000 debt, the debt is not paid off, and there is a 10% interest on the debt, the debt can compound in the same way. Some student loans are structured this way, where payments can be deferred until after graduation, but interest keeps accumulating on the debt while you are in college. If you take out this type of loan but don’t start paying it down until after college, more debt accumulates, resulting in more money owed than the total amount borrowed.
Here is the formula for compound interest. It demonstrates the number of variables that contribute to the total compounded.
A = P(1+(r/n)^nt
A-total amount accumulated after n years
P-Principal amount (initial deposit)
r-annual rate of interest (decimal)
n-number of times compounded per year
t-number of years the amount is deposited
If you are interested in seeing different scenarios for compounding interest, you can use the free calculator and begin preparing to invest with compounding interest today.